Query Optimization

Evaluation Plan defines the algorithm that is used for each operation, and how they would be co-ordinated. It is usually represented as a tree. Ideally, we would like to chose the cheapest plan based on its estimated cost.

PostgreSQL shows cost as $f..l$ where $f$ is the cost of delivering the first tuple and $l$ is the cost for delivering all the tuples

Generating Equivalent Rules

Two rules are equivalent if they generate the same set of tuples for every legal dataset instance.

Conjunction: $\sigma_{\theta_1\wedge\theta_2}(E) \equiv \sigma_{\theta_1}(\sigma_{\theta_2}(E))$
Commutative Selection: $\sigma_{\theta_1}(\sigma_{\theta_2}(E)) \equiv \sigma_{\theta_2}(\sigma_{\theta_1}(E))$
Commutative Joins: $E_1\bowtie E_2 \equiv E_2\bowtie E_1$
Subset Projection: $\Pi_{L_1}(\Pi_{L_2}(E)) \equiv \Pi_{L_1}(E)$ if $L_1\subseteq L_2$
Selections with Products/Joins:
1. $\sigma_{\theta_1}(E_1\times E_2) \equiv E_1 \bowtie_{\theta_1}E_2$
2. $\sigma_{\theta_1}(E_1\bowtie_{\theta_2} E_2) \equiv E_1\bowtie_{\theta_1\wedge\theta_2} E_2)$
Join Associativity:
1. $(E_1\bowtie E_2)\bowtie E_3 \equiv E_1\bowtie (E_2\bowtie E_3)$ - Natural Joins are associative
2. $(E_1\bowtie_{\theta_1} E_2)\bowtie_{\theta_2\wedge\theta_3} E_3 \equiv E_1\bowtie_{\theta_1\wedge\theta_3} (E_2\bowtie_{\theta_2} E_3)$ - $\theta_2$ contains attributes only from $E_2, E_3$
Select Distribution over Join:

$\sigma_{\theta_1\wedge\theta_2}(E_1\bowtie_\theta E_2) \equiv \sigma_{\theta_1}(E_1)\bowtie_\theta\sigma_{\theta_2}(E_2)$ - $\theta_1$ has attributes of only $E_1$ and $\theta_2$ only of $E_2$
Project Distribution over Join:

Consider $\Pi_{L_1\cup L_2}(E_1\bowtie_\theta E_2)$, where $L_1$ are attributes of $E_1$ and $L_2$ of $E_2$. Let $L_3$ be the set of attributes that are used in the condition $\theta$ but do not belong to $L_1$, and similarly define $L_4$ for $E_2$.

$\Pi_{L_1\cup L_2}(E_1\bowtie_\theta E_2) \equiv \Pi_{L_1\cup L_3}\left( \Pi_{L_1\cup L_3}(E_1)\bowtie_\theta\Pi_{L_2\cup L_4}(E_2) \right)$
Union and Intersection are Commutative
Union and Intersection are Associative
Select Operation distributes over Union, Intersection and Difference

==slides have additional relations that I didn’t get here!==
Projection is Distributive over Union: $\Pi_L(E_1\cup E_2) \equiv \Pi_L(E_1)\cup\Pi_L(E_2)$
Selection Distributes over Aggregate: $\sigma_\theta(G\gamma_A(E)) = {}_G\gamma_A(\sigma\theta(E))$ ==provided $\theta$ only involves attributes in $G$==
Outer Join Commutativity: (They are NOT associative in nature!)
1. $E_1 ⟗ E_2 = E_2 ⟗ E_1 $
2. $E_1 ⟕ E_2 = E_2 ⟖ E_1$ ==Note different outer join!==
Selection Distributes over Outer joins:
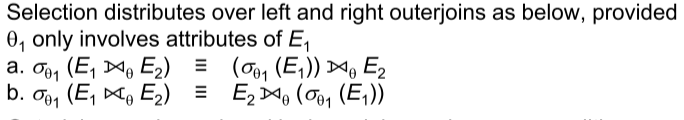
Replacing outer joins with inner joins:

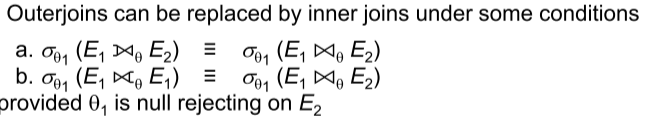
Cost Based Optimization of Evaluation Plans

Join Ordering

\[(a\bowtie b)\bowtie c \equiv a\bowtie(b\bowtie c)\]

Here, if $(a\bowtie b)$ is larger than $(b\bowtie c)$ we choose to compute using the right equation so we store a smaller relation temporarily. Now consider the more general case: $r_1\bowtie r_2 \ldots \bowtie r_n$ We use dynamic programming to efficiently compute the cost. Let $S = {r_1, \ldots r_n}$. We consider all possible plans of form $S’\bowtie(S-S’)$ where $S’$ is a non-empty subset of $S$. Recurse on $S’$, storing the costs of every subset and not recomputing them everytime. The complexity of this method would be exponential $\mathcal{O}(3^n)$.

However, if we consider only LEFT-DEEP subtrees, the complexity becomes $\mathcal{O}(n2^n)$.

==merge join may be beneficial as sorted attributes make further joins easier!==

Heuristic Optimization

Cost based optimization can be expensive both memory-wise and time-wise. Most optimizers use heuristics that usually tend to reduce execution time.

Perform selections and projections early
Perform restrictive selections and joins first
Use left deep join trees

Statistical Cost Estimation

Symbol	Meaning
$n_r$	Number of tuples in Relation $r$
$b_r$	Number of blocks containing tuples of $r$
$l_r$ or $s_r$	Size of a tuple $r$
$f_r$	Blocking Factor, number of tuples that fit into one block. $b_r = \lceil n_r/f_r\rceil$
$V(A,r)$	Number of distinct values of attribute $A$ of relation $r$

Size Estimation

$\sigma_{A=v}(r)$

Assume each distinct value has approximately equal number of rows. The number of records returned would be $n_r/V(A,r)$
$\sigma_{A\leq v}(r)$

Assume $\min(A,r)$ and $\max(A,r)$ are known. Assume that the tuples are distributed linearly. The estimated number of tuples would be: $\frac{v-\min(A,r)}{\max(A,r)-\min(A,r)}\times n_r$ We estimate $n_r/2$ if the information is absent.

Selectivity

The selectivity of a condition $\theta$ is the probability that a tuple in $r$ satisfies $\theta$. If the satisfying tuples are $s_\theta$, selectivity would be $s_\theta/n_r$.

$\sigma_{\theta_1\wedge\theta_2\ldots\theta_n}(r)$ $\text{Selectivity} = \frac{s_1\times \ldots s_n}{n_r^n}$
$\sigma_{\theta_1\lor\theta_2\ldots\theta_n}(r)$ $\text{Selectivity} = 1-\left[ \left(1-\frac{s_1}{n_r}\right)\ldots\left(1-\frac{s_n}{n_r}\right) \right]$
$\sigma_{\neg\theta}(r)$: $1-\frac{s_\theta}{n_r}$

Join Size Estimation

==Multiple Cases about something….==

Other Operations

Estimated size of $\Pi_{A}(r)$: $V(A,r)$
Estimated size of ${}_G\gamma_A(r)$: $V(G,r)$
Estimated size of $r⟕s$: size of $r\bowtie s$ + size of $r$
Estimated size of $r⟗s$: size of $r\bowtie s$ + size of $r$ + size of $s$

Distinct Value Estimation

$\sigma_\theta(r)$
1. $\theta$ forces $A$ to take a specific value - $V(A,\sigma_\theta(r))=1$
2. $\theta$ forces $A$ to take multiple specified values - $V(A,\sigma_\theta(r))=$num values specified
3. $\theta$ is of form $A\text{ op }r$ - $V(A,\sigma_\theta(r)) = V(A,r)\times \text{selectivity}_\theta$
4. In all other cases - $V(A,\sigma_\theta(r)) = \min(V(A,r), n_{\sigma_\theta(r)})$
$r\bowtie s$

Let $A$ contain $A_1$ from $r$ and $A_2$ from $s$. The estimate would be given by: $V(A,r\bowtie s) = \min(V(A_1,r)\cdot V(A_2-A_1,s), n_{r\bowtie s}, V(A_1-A_2,r)\cdot V(A_2,s))$

Optimizing Nested Subqueries

The variables of the outer queries that are used by the nested queries are called as correlation variables. Usually, the nested subquery is executed once for every tuple in the from clause’s relation. This is called correlated evaluation, and is very inefficient!

Usually, we try to use joins instead of subqueries, but this can cause different number of duplicates. We introduce the semi-join operator to solve this problem.

In general, SQL queries of the following form are written using semi joins.

select A
from r1, r2, ... rn
where P1 and exists (select *
                     from s1, s2, ... sm
                     where P21 and P22)

Here, $P21$ contains the predicates that do not involve correlation variables, and $P22$ has predicates that contain correlation variables. This can be written as: $\Pi_A\left[ \sigma_{P1}(r1\times r2\ldots rn) \ltimes_{P22}\sigma_{P21}(s1\times s2\ldots sm) \right]$ This process of replacing the nested query is called as decorrelation.

This example is quite important, try working in a bottom-up manner to get the final relational algebra query.

Materialized Views

A view whose contents are computed and stored are called as materialized views. Keeping it upto date with the underlying data is called as maintenance. Incremental maintenance computes the updates everytime the database is updated.

The changes to a relation or expression are called as its differential.

Join Operation

Consider the relation $v = r\bowtie s$, with $r_{new}$ being the updated data and $r_{old}$ being the outdated data. Outer joins are handled similarly with additional cases.

Inserts - $v_{new} = v_{old} \cup(i_r\bowtie s)$
Deletes -$v_{new} = v_{old} -(d_r\bowtie s)$

Selection Operation

Very similar to the ones used in join operation. Let the view be $v = \sigma_\theta(r)$.

Inserts - $v_{new} = v_{old} \cup\sigma_\theta(i_r)$
Deletes -$v_{new} = v_{old} -\sigma_\theta(d_r)$

Projection Operation

Let the view be $v = \Pi_A(r)$. Keep a count of each tuple in the view, and update the corresponding count when a row is deleted in $r$. Delete the tuple from the view when the count hits 0.

Aggregation Operation

Count: $v = {}A\gamma{count(B)}(r)$

Update the count/add a new tuple when a new row is added into $r$. Delete the tuple when count is 0.
Sum: $v = {}A\gamma{Sum(B)}(r)$

Maintain both count and sum for each tuple, and update accordingly. Delete when the count of a tuple is 0. Similarly for average, divide them when value is requested.

Expressions are handled by computing the incremental change for the sub-expressions and propagating the changes in a bottom-up manner.

Akash Cherukuri